Funkce
Pochopení
- je to přepis, který z hodnot jedné proměnné (x) jednoznačně (jedna hodnota) vytvoří číslo z druhé proměnné
- to, co do funkce vkládám jsou nezávislé proměnné (označují se "x"), to co dostanu jsou závislé proměnné (návisí na nezávislé proměnné, zonbačují se "y")
- příklad: Chci si koupit 5 rohlíku, jeden rohlík stojí 3 koruny. Funkce bude: 3x = y (x je počet, y je cena, kterou dostanu). Výsledek: zaplatím 15 Kč
Pro programátory (C#)
jen pro zajímavost
static int CenaRohliku(int PocetRohliku)
{
return 3 * PocetRohliku;
}
v matematice se toto zapisuje jako 3x = y (x = 5), stejného bychom docílili s CenaRohliku(5);
Zápisy
(pro získání ceny, když si koupím 5 rohlíků, jeden stojí 3 Kč)
Předpis
y = 3x
f: y = 3x
f(x) = 3x
Tabulka
| proměnná | ||||
|---|---|---|---|---|
| počet x | 1 | 2 | 3 | 4 |
| cena y | 3 | 6 | 9 | 12 |
Graf
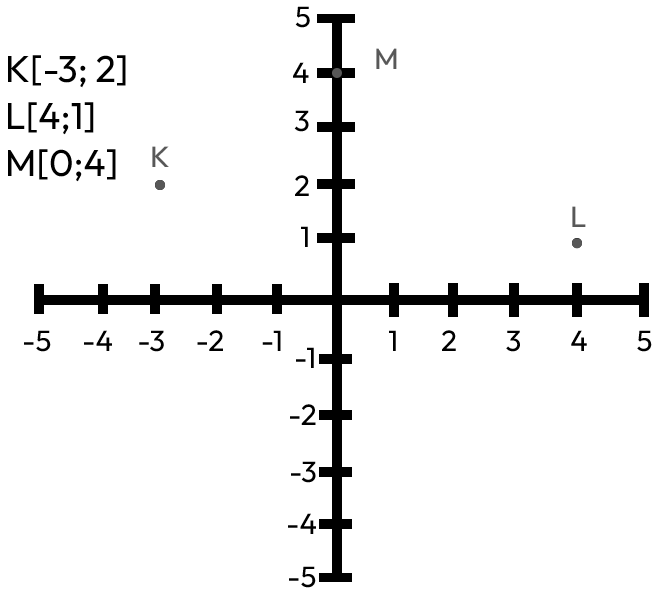
Pojmy
Definiční obor funkce
- všechna čísla x, která můžu vložít do funkce
D(f) = {1; 2; 3; 4; ..}
Obor hodnot funkce
- všechna čísla y, která mohu získat pomocí x
H(f) = {3; 6; 9; 15; ..}
Intervaly
- zápis všech čísel mezi určitým rozmezím (včetně/bez krajních čísel)
| Typ intervalu | Závorky | Nerovnostní zápis | Popis |
|---|---|---|---|
| Otevřený | (a, b) | a < x < b | Body nepatří do intervalu |
| Uzavřený | ⟨a, b⟩ | a ≤ x ≤ b | Body patří do intervalu |
| Polouzavřený zleva | ⟨a, b) | a ≤ x < b | Levý bod patří, pravý nepatří do intervalu |
| Polouzavřený zprava | (a, b⟩ | a < x ≤ b | Levý bod nepatří, pravý patří do intervalu |
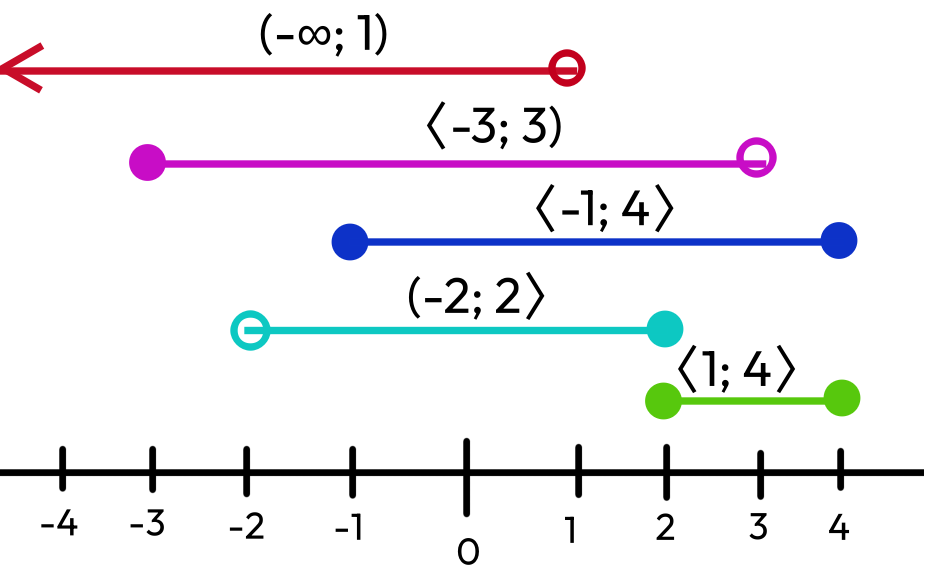
Graf funkce

- více o soustavě zde
Přímá úměrnost
- vysvětlení a další informace zde
- kolikrát se zvětší/změnší x, tolikrát se zvětší/zmenší y
- předpis: y = k × x; k ≠ 0
- příklady - cena rohlíků, dráha na čase, obvod kružnice
| proměnná | |||
|---|---|---|---|
| x | 1 | 2 | 3 |
| y | 20 | 40 | 60 |
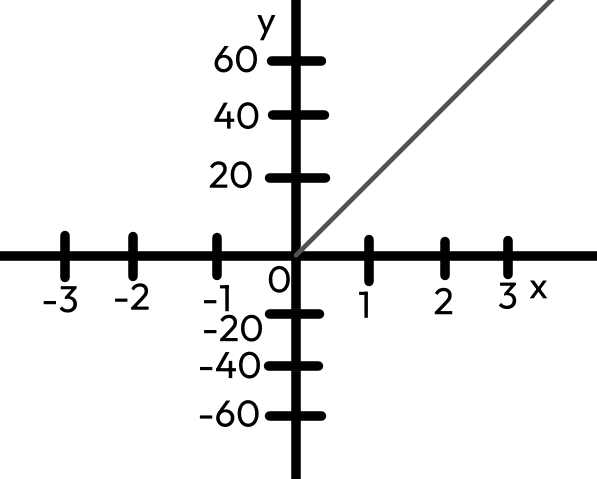 graf přímé úměrnosti
graf přímé úměrnosti
- při zvýšení/snížení k se sklon změní
Klesající
y = -k × x; k < 0
| proměnná | ||
|---|---|---|
| x | 1 | 2 |
| y | -1 | -2 |
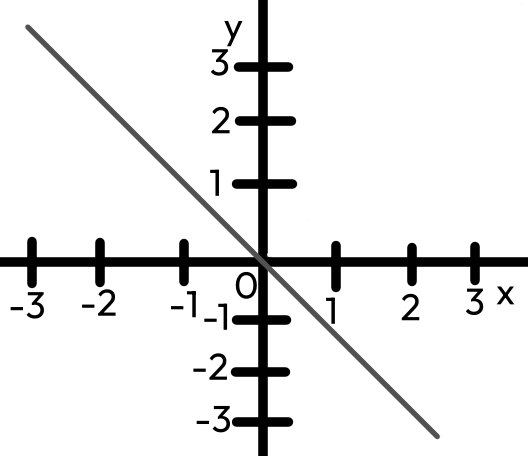
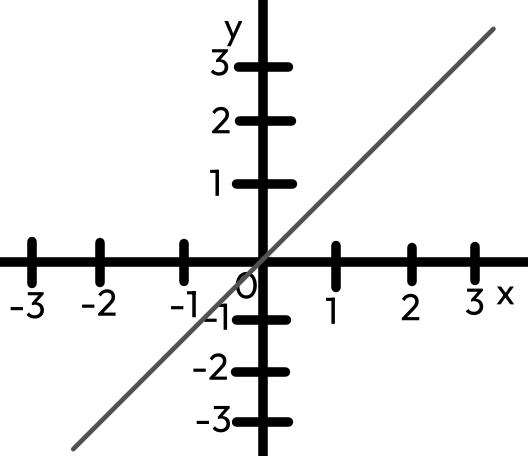
Rostoucí
y = k × x; k > 0
| proměnná | ||
|---|---|---|
| x | 1 | 2 |
| y | 1 | 2 |
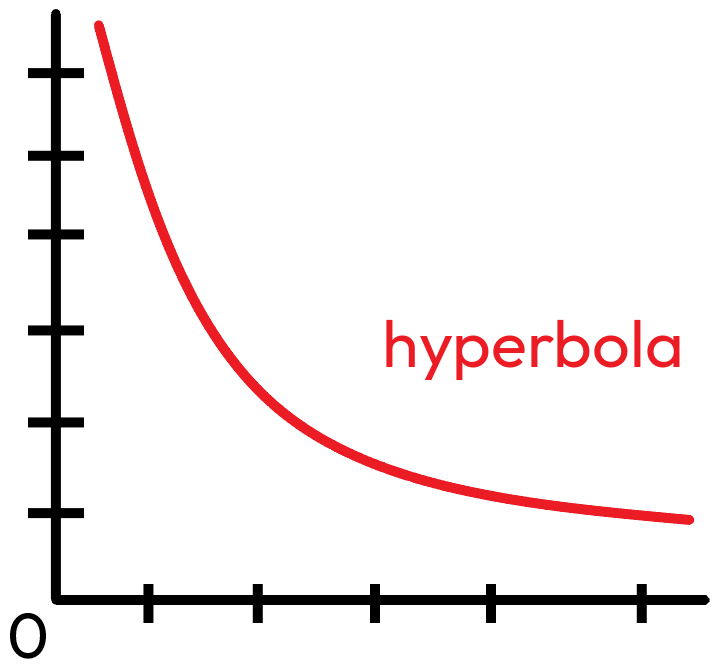
Nepřímá úměrnost
- vysvětlení a další informace zde
- kolikrát se zvětší/zmenší x, tolikrát se zmenší/zvětší y
- předpis: y = ; k ≠ 0
- grafem je hyperbola, v 1. a 3. kvadrantu při kladném k, při záporném je v 2. a 4. kvadrantu
- čím více se k zvětší/změnší, tím míň/víc je hyperbola blíž k osám
x .. počet dělníků
y .. čas [den]
| proměnná | ||||||
|---|---|---|---|---|---|---|
| x | 1 | 2 | 4 | 5 | 10 | 20 |
| y | 20 | 10 | 5 | 4 | 2 | 1 |
Lineární funkce
- k, q - libovolná čísla
- q je proměnná, která určuje "výšku"
- Df = ℝ (reálné číslo)
- Hf = ℝ (reální číslo)
y = k × x + q
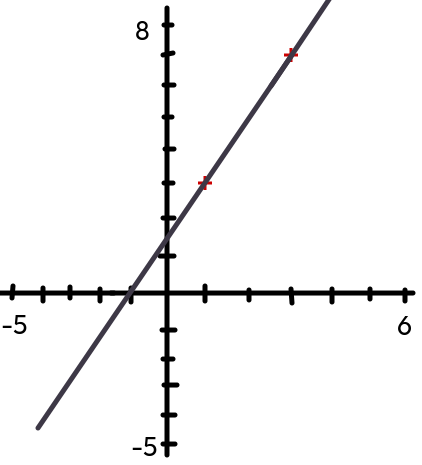
y = 2x + 1
| proměnná | ||
|---|---|---|
| x | 1 | 3 |
| y | 3 | 7 |
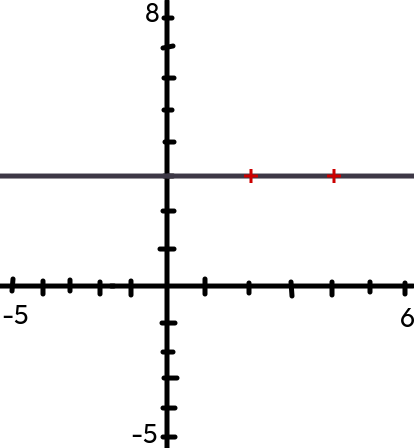
Konstantní funkce
- je-li k = 0, pak y = q
k = 0
q = 3
y = 0x + 3
y = 3
| proměnná | ||
|---|---|---|
| x | 2 | 4 |
| y | 3 | 3 |
Určení předpisu lineární funkce
y = kx + q
- vyberu 2 dvojice bodů a vyřeším 2 soustavy
- zapíšu předpis
1.
| proměnná | ||||
|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 |
| y | 3 | 4 | 5 | 6 |
3 = k × 0 + q
4 = k × 1 + q
3 = q
4 = k + 1 = k
předpis: y = x + 3
2.
| proměnná | |||
|---|---|---|---|
| x | 1 | 2 | 3 |
| y | 3 | 5 | 2 |
3 = 1 × k + q
5 = 2 × k + q
3 = k +
3 - q = k
5 = 2 × (3 - q) + q
5 = 6 - 2q + q
5 = 6 -
-1 = -q
1 = q
3 - q = k
3 - 1 = k
2 = k
y = 2x + 1
Prusečíky s osami
Px - průsečík s osou x, Py - průsečík s osou y
Px [x; 0]
Py [0, y]
Najdi průsečíky os u funkce y = 3x - 2
vyřešíme rovnice pro x a y, když je to druhé 0
0 = 3x - 2 / +2
2 = 3x / ÷3
= x
y = 3 × 0 - 2 y = -2
Px [; 0] Py [0, -2]